Механическое движение: изучаем вместе

Время чтения 10 минут

Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.

Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.

Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.

Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.

Тело, относительно которого рассматривается движение, называется телом отсчёта.

Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.

Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.

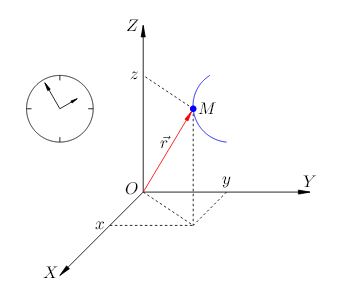
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат . Начало координат является телом отсчёта.

Вектор $\vec{r} = \overrightarrow{OM}$ называется радиус-вектором точки . Координаты точки являются в то же время координатами её радиус-вектора .

Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: .

В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.

Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.

К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.

Содержание скрыть

1 Траектория, путь, перемещение.

2 Скорость и ускорение.

3 Закон сложения скоростей.

4 Виды механического движения.

Траектория, путь, перемещение.

В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.

Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора .

Путь — это длина участка траектории, пройденного телом за данный промежуток времени.

Перемещение — это вектор, соединяющий начальное и конечное положение тела.

Предположим, что тело начало движение в точке и закончило движение в точке (рис. 2). Тогда путь, пройденный телом, это длина траектории . Перемещение тела — это вектор $\overrightarrow{AB} = \overrightarrow{OM}$ .

Скорость и ускорение.

Рассмотрим движение тела в прямоугольной системе координат с базисом $\vec{i}, \vec{j}, \vec{k}$ (рис. 3).

Пусть в момент времени тело находилось в точке с радиус-вектором

\overrightarrow{OM}=\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}

Спустя малый промежуток времени $\Delta t$ тело оказалось в точке $N(x+\Delta x,y+\Delta y,z+\Delta z)$ с

радиус-вектором

\overrightarrow{ON}=\vec{r}+\Delta \vec{r}=(x+\Delta x)\vec{i}+(y+\Delta y)\vec{j}+(z+\Delta z)\vec{k}

Перемещение тела:

$\Delta r=\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=(\Delta x)\vec{i}+(\Delta y)\vec{j}+(\Delta z)\vec{k}$ (1)

Мгновенная скорость $\Delta v$ в момент времени – это предел отношения перемещения $\Delta \vec{r}$ к интервалу времени $\Delta t$ , когда величина этого интервала стремится к нулю; иными словами, скорость точки – это производная её радиус-вектора:

$\vec{v}=\frac{\displaystyle \Delta \vec{\displaystyle r}}{\displaystyle \Delta \displaystyle t}=\frac{\displaystyle d\vec{r}}{\displaystyle dt}$ (2)

Из (2) и (1) получаем:

\vec{v}=\lim_{\Delta t\rightarrow 0}\left ( \frac{\displaystyle \Delta \displaystyle x}{\displaystyle \Delta \displaystyle t}\vec{\displaystyle i}+\frac{\displaystyle \Delta \displaystyle y}{\displaystyle \Delta \displaystyle t}\vec{\displaystyle j}+\frac{\displaystyle \Delta \displaystyle z}{\displaystyle \Delta \displaystyle t}\vec{\displaystyle k} \right )

Коэффициенты при базисных векторах в пределе дают производные:

\dot{x}=\lim_{\Delta t\rightarrow 0}\frac{\displaystyle \Delta \displaystyle x}{\displaystyle \Delta \displaystyle t}, \dot{y}=\lim_{\Delta t\rightarrow 0}\frac{\displaystyle \Delta \displaystyle y}{\displaystyle \Delta \displaystyle t}, \dot{z}=\lim_{\Delta t\rightarrow 0}\frac{\displaystyle \Delta \displaystyle z}{\displaystyle \Delta \displaystyle t}

(Производная по времени традиционно обозначается точкой над буквой.) Итак,

Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:

\displaystyle v_{\displaystyle x}=\dot{x}, \displaystyle v_{\displaystyle y}=\dot{y}, \displaystyle v_{\displaystyle z}=\dot{z}.

Когда $\Delta t$ стремится к нулю, точка приближается к точке и вектор перемещения $\Delta \vec{r}$ разворачивается в направлении касательной. Оказывается, что в пределе вектор $\Delta \vec{v}$ направлен точно по касательной к траектории в точке . Это и показано на рис. 3.

Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна $\vec{v}$ , а спустя малый интервал $\Delta t$ скорость стала равна $\vec{v}+\Delta \vec{v}$ .

Ускорение $\vec{a}$ – это предел отношения изменения скорости $\Delta \vec{v}$ к интервалу $\Delta {t}$ , когда этот интервал стремится к нулю; иначе говоря, ускорение – это производная скорости:

\vec{a}=\lim_{\Delta t\rightarrow 0}\frac{\displaystyle \Delta \vec{\displaystyle v}}{\displaystyle \Delta \displaystyle t}=\frac{\displaystyle d\vec{\displaystyle a}}{\displaystyle dt}.

Ускорение, таким образом, есть “cкорость изменения скорости”. Имеем:

\vec{a}=\frac{\displaystyle d}{\displaystyle dt}(\displaystyle v_{\displaystyle x}\vec{\displaystyle i}+\displaystyle v_{\displaystyle y}\vec{\displaystyle j}+\displaystyle v_{\displaystyle z}\vec{\displaystyle k})=\dot{\displaystyle v_{\displaystyle x}}\vec{\displaystyle i}+\dot{\displaystyle v_{\displaystyle y}}\vec{\displaystyle j}+\dot{v_{\displaystyle z}}\vec{\displaystyle k}.

Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):

\displaystyle a_{\displaystyle x}=\dot{\displaystyle v_{\displaystyle x}}=\ddot{\displaystyle x}, \displaystyle a_{\displaystyle y}=\dot{\displaystyle v_{\displaystyle y}}=\ddot{\displaystyle y}, \displaystyle a_{\displaystyle z}=\dot{\displaystyle v_{\displaystyle z}}=\ddot{\displaystyle z}.

Закон сложения скоростей.

Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной.

Вторая система отсчёта, обозначаемая , связана с телом отсчёта , которое движется относительно тела со скоростью $\vec{u}$ . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы перемещаются параллельно самим себе (нет вращения системы координат), так что вектор $\vec{u}$ можно считать скоростью движущейся системы относительно неподвижной.

Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью $\vec{u}$ , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта .

Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна $\vec{u}$ . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью $\vec{u}$ . Муха переносится вагоном, и потому скорость $\vec{u}$ движущейся системы относительно неподвижной называется переносной скоростью.

Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается ${\vec{v}}$ и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается $\vec{v}$ и называется абсолютной скоростью.

Выясним, как связаны друг с другом эти три скорости – абсолютная, относительная и переносная.

На рис. 4 муха обозначена точкой .Далее:

$\vec{r}$ – радиус-вектор точки в неподвижной системе ;

${\vec{r}}$ – радиус-вектор точки в движущейся системе ;

$\vec{R}$ – радиус-вектор тела отсчёта в неподвижной системе .

Как видно из рисунка,

Дифференцируя это равенство, получим:

$\frac{\displaystyle d\vec{\displaystyle r}}{\displaystyle dt}=\frac{\displaystyle d\vec{\displaystyle R}}{\displaystyle dt}+\frac{\displaystyle d{\vec{\displaystyle r}}$ (3)

(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).

Производная $d\vec{r}/dt$ есть скорость точки в системе , то есть абсолютная скорость:

$\frac{\displaystyle d\vec{\displaystyle r}}{\displaystyle dt}=\vec{v}$ .

Аналогично, производная $d{\vec{r}}$ есть скорость точки в системе , то есть относительная скорость:

А что такое $d\vec{R}/dt$ ? Это скорость точки в неподвижной системе, то есть – переносная скорость $\vec{u}$ движущейся системы относительно неподвижной:

\frac{\displaystyle d\vec{\displaystyle R}}{\displaystyle dt}=\vec{u}

В результате из (3) получаем:

Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.

Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!

Виды механического движения.

Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.

Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).

Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.

Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.

А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.

В терминах вектора скорости можно дать более короткие определения данным типам движения:

равномерное движение $\Leftrightarrow |\vec{v}|=const$
прямолинейное движение $\Leftrightarrow \frac{\displaystyle v}{|\vec{\displaystyle v}|}=const$
равномерное прямолинейное движение $\Leftrightarrow \vec{v}=const$

Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:

равноускоренное движение $\Leftrightarrow \vec{a}=const$

Наряду с материальной точкой в механике рассматривается ещё одна идеализация – твёрдое тело.

Твёрдое тело – это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.

Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.

Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).

Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.

На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.

Механическое движение

Траектория, путь, перемещение.

Скорость и ускорение.

Закон сложения скоростей.

Виды механического движения.

Добавить комментарий Отменить ответ

Подготовка к ЕГЭ

Задание 38 на ЕГЭ по химии

Задания на гидролиз (№30) в ЕГЭ по химии

Задача С5 на ЕГЭ по химии. Определение формул органических веществ

Задачи на смеси и сплавы на ЕГЭ по химии

Задания С2 из вариантов ЕГЭ по химии для самостоятельной работы