Сила тяготения: изучаем вместе

Время чтения 6 минут

Темы кодификатора ЕГЭ: силы в механике, закон всемирного тяготения, сила тяжести, ускорение свободного падения, вес тела, невесомость, искусственные спутники Земли.

Любые два тела притягиваются друг к другу – по той лишь одной причине, что они имеют массу. Эта сила притяжения называется силой тяготения или гравитационной силой.

Содержание скрыть

1 Закон всемирного тяготения.

2 Сила тяжести.

3 Вес тела. Невесомость.

4 Искусственные спутники.

Закон всемирного тяготения.

Гравитационное взаимодействие любых двух тел во Вселенной подчиняется достаточно простому закону.

Закон всемирного тяготения. Две материальные точки массами $m_{\displaystyle 1}$ и $m_{\displaystyle 2}$ притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:

$F=G\frac{\displaystyle m_{\displaystyle 1}\displaystyle m_{\displaystyle 2}}{\displaystyle r^{\displaystyle 2}}.$ (1)

Коэффициент пропорциональности называется гравитационной постоянной. Это фундаментальная константа, и её численное значение было определено на основе эксперимента Генри Кавендиша:

G=6.67\cdot 10^{-11} \cdot \frac{\displaystyle H\cdot \displaystyle m^{\displaystyle 2}}{\displaystyle kg^{\displaystyle 2}}.

Порядок величины гравитационной постоянной объясняет, почему мы не замечаем взаимного притяжения окружающих нас предметов: гравитационные силы оказываются слишком малыми при небольших массах тел. Мы наблюдаем лишь притяжение предметов к Земле, масса которой примерно $6\cdot 10^{24}$ кг.

Формула (1), будучи справедливой для материальных точек, перестаёт быть верной, если размерами тел пренебречь нельзя. Имеются, однако, два важных для практики исключения.

1. Формула (1) справедлива, если тела являются однородными шарами. Тогда – расстояние между их центрами. Сила притяжения направлена вдоль прямой, соединяющей центры шаров.

2. Формула (1) справедлива, если одно из тел – однородный шар, а другое – материальная точка, находящаяся вне шара. Тогда сстояние от точки до центра шара. Сила притяжения направлена вдоль прямой, соединяющей точку с центром шара.

Второй случай особенно важен, так как позволяет применять формулу (1) для силы притяжения тела (например, искусственного спутника) к планете.

Сила тяжести.

Предположим, что тело находится вблизи некоторой планеты. Сила тяжести – это сила гравитационного притяжения, действующая на тело со стороны планеты. В подавляющем большинстве случаев сила тяжести – это сила притяжения к Земле.

Пусть тело массы лежит на поверхности Земли. На тело действует сила тяжести , где – ускорение свободного падения вблизи поверхности Земли. С другой стороны, считая Землю однородным шаром, можно выразить силу тяжести по закону всемирного тяготения:

$mg=G\frac{\displaystyle Mm}{\displaystyle R^{\displaystyle 2}}$ ,

где – масса Земли, $R\approx 6400$ км – радиус Земли. Отсюда получаем формулу для ускорения свободного падения на поверхности Земли:

$g= G \frac {M}{R^{\displaystyle 2}}$ . (2)

Эта же формула, разумеется, позволяет найти ускорение свободного падения на поверхности любой планеты массы и радиуса .

Если тело находится на высоте над поверхностью планеты, то для силы тяжести получаем:

$mg(h)=G\frac{\displaystyle mM}{\displaystyle (R+h)^{\displaystyle 2}}$ .

Здесь – ускорение свободного падения на высоте :

$g(h)=G\frac{\displaystyle M}{\displaystyle (R+h)^{\displaystyle 2}}=\frac{\displaystyle gR^{2}}{\displaystyle (R+h)^{\displaystyle 2}}$ .

В последнем равенстве мы воспользовались соотношением

которое следует из формулы (2).

Вес тела. Невесомость.

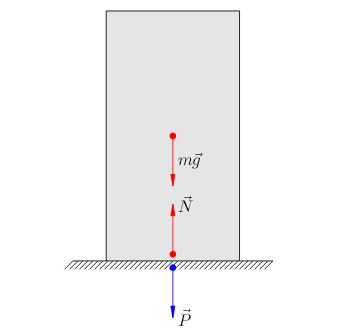
Рассмотрим тело, находящееся в поле силы тяжести. Предположим, что есть опора или подвес, препятствующие свободному падению тела. Вес тела – это сила, с которой тело действует на опору или подвес. Подчеркнём, что вес приложен не к телу, а к опоре (подвесу).

На рис. 1 изображено тело на опоре. Со стороны Земли на тело действует сила тяжести $m\vec{g}$ (в случае однородного тела простой формы сила тяжести приложена в центре симметрии тела). Со стороны опоры на тело действует сила упругости $\vec{N}$ (так называемая реакция опоры). На опору со стороны тела действует сила $\vec{P}$ – вес тела. По третьему закону Ньютона силы $\vec{P}$ и $\vec{N}$ равны по модулю и противоположны по направлению.

Предположим, что тело покоится. Тогда равнодействующая сил, приложенных к телу, равна нулю. Имеем:

m\vec{g}+\vec{N}=\vec{0}\Rightarrow m\vec{g}=-\vec{N}\Rightarrow mg=N.

С учётом равенства получаем . Стало быть, если тело покоится, то его вес равен по модулю силе тяжести.

Задача. Тело массы вместе с опорой движется с ускорением , направленным вертикально вверх. Найти вес тела.

Решение. Направим ось вертикально вверх (рис. 2).

Запишем второй закон Ньютона:

Перейдём к проекциям на ось :

Отсюда . Следовательно, вес тела

Как видим, вес тела больше силы тяжести. Такое состояние называется перегрузкой.

Задача. Тело массы вместе с опорой движется с ускорением $a\leqslant g$ , направленным вертикально вниз. Найти вес тела.

Решение. Направим ось вертикально вниз (рис. 3).

Схема решения та же. Начинаем со второго закона Ньютона:

Переходим к проекциям на ось :

Отсюда c. Следовательно, вес тела

В данном случае вес тела меньше силы тяжести. При (свободное падение тела с опорой) вес тела обращается в нуль. Это – состояние

невесомости, при котором тело вообще не давит на опору.

Искусственные спутники.

Для того, чтобы искусственный спутник мог совершать орбитальное движение вокруг планеты, ему нужно сообщить определённую скорость. Найдём скорость кругового движения спутника на высоте над поверхностью планеты. Масса планеты , её радиус (рис. 4)

Спутник будет двигаться под действием единственной силы $\vec{F}$ – силы всемирного тяготения, направленной к центру планеты. Туда же направлено и ускорение спутника – центростремительное ускорение