Равномерное движение по окружности

Нет комментариев
   Время чтения 2 минуты

Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.

Равномерное движение по окружности – это достаточно простой пример движения с вектором ускорения, зависящим от времени.

Пусть точка вращается по окружности радиуса r. Скорость точки постоянна по модулю и равна v. Скорость v называется линейной скоростью точки.

Период обращения – это время одного полного оборота. Для периода T имеем очевидную формулу:

T=\frac{\displaystyle 2\pi r}{\displaystyle v}. (1)

Частота обращения – это величина, обратная периоду:

\nu =\frac{\displaystyle 1}{\displaystyle T}.

Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).

Пусть, например, T=0,1 c. Это означает, что за время 0,1 c точка совершает один полный

оборот. Частота при этом получается равна: \nu = 1/0,1 = 10 об/с; за секунду точка совершает 10 полных оборотов.

Содержание скрыть
1 Угловая скорость.
2 Закон движения.
3 Центростремительное ускорение.

Угловая скорость.

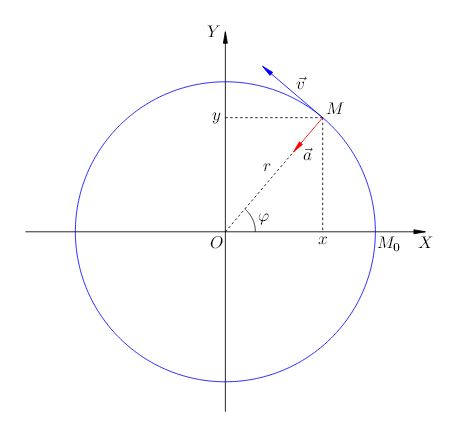
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).

Рис. 1. Равномерное движение по окружности

Пусть M_{0} – начальное положение точки; иными словами, при t = 0 точка имела координаты (r, 0). Пусть за время t точка повернулась на угол \varphi и заняла положение M.

Отношение угла поворота ко времени называется угловой скоростью вращения точки:

\omega =\frac{\displaystyle \varphi }{\displaystyle t}. (2)

Угол \varphi, как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол 2\pi . Поэтому

\omega =\frac{\displaystyle 2\pi }{\displaystyle t}. (3)

Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:

v= \omega r. (4)

Закон движения.

Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что

x=r cos \varphi, y=r sin \varphi.

Но из формулы (2) имеем: \varphi= \omega t. Следовательно,

x=r cos \omega t, y=r sin \omega t. (5)

Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.

Центростремительное ускорение.

Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):

v_{\displaystyle x}=\dot{x}=-\omega r sin \omega t, v_{\displaystyle y}=\dot{y}=\omega r cos\omega t,
a_{x}=\dot{v_{x}}=-\omega ^{2}rcos\omega t, a_{y}=\dot{v}y=-\omega ^{2}rsin\omega t.

С учётом формул (5) имеем:

a_{x}=-\omega^{2}x, a_{y}=-\omega^{2}y. (6)

Полученные формулы (6) можно записать в виде одного векторного равенства:

\vec{a}=-\omega^{2}\vec{r}, (7)

где \vec{r} – радиус-вектор вращающейся точки.

Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.

Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:

a=\omega^{2}r. (8)

Выразим угловую скорость из (4)

\omega =\frac{\displaystyle v}{\displaystyle r}

и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:

a=\frac{\displaystyle v^{2}}{\displaystyle r}.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

два × два =