Путь при неравномерном движении

Сейчас мы будем рассматривать неравномерное движение – то есть движение, при котором абсолютная величина скорости меняется со временем. Оказывается, существует простая геометрическая интерпретация пути, пройденного телом при произвольном движении.

Начнём с равномерного движения. Пусть скорость тела постоянна и равна . Возьмём два момента времени: начальный момент и конечный момент . Длительность рассматриваемого промежутка времени равна .

Очевидно, что за промежуток времени тело проходит путь:

(1)

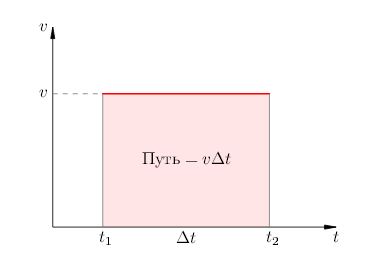
Давайте построим график зависимости скорости от времени. В данном случае это будет прямая, параллельная оси абсцисс (рис. 1).

Рис. 1. Путь при равномерном движении

Нетрудно видеть, что пройденный путь равен площади прямоугольника, расположенного под графиком скорости. В самом деле, первый множитель в формуле (1) есть вертикальная сторона этого прямоугольника, а второй множитель – его горизонтальная сторона.

Теперь нам предстоит обобщить эту геометрическую интерпретацию на случай неравномерного движения.

Пусть скорость тела зависит от времени, и на рассматриваемом промежутке график скорости выглядит, например, так (рис. 2):

Рис. 2. Неравномерное движение

Дальше мы рассуждаем следующим образом.

1. Разобьём наш промежуток времени на небольшие отрезки величиной .

2. Предположим, что на каждом таком отрезке тело движется с постоянной скоростью . То есть, плавное изменение скорости заменим ступенчатой аппроксимацией*: в течение каждого небольшого отрезка времени тело движется равномерно, а затем скорость тела мгновенно и cкачком меняется.

На рис. 3 показаны две ступенчатые аппроксимации. Ширина ступенек на правом рисунке вдвое меньше, чем на левом.

Рис. 3. Ступенчатая аппроксимация

Путь, пройденный за время равномерного движения – это площадь прямоугольника, расположенного под ступенькой. Поэтому путь, пройденный за всё время такого “ступенчатого” движения – это сумма площадей всех прямоугольников на графике.

3. Теперь устремляем к нулю. Ясно, что в пределе наша ступенчатая аппроксимация перейдёт в исходный график скорости на рис. 2. Сумма площадей прямоугольников перейдёт в площадь под графиком скорости; следовательно, эта площадь и есть путь, пройденный телом за время от до . (рис. 4

Рис. 4. Путь при неравномерном движении

В итоге мы приходим к нужному нам обобщению геометрической интерпретации пути, полученной выше для случая равномерного движения.

Аппроксимация – это приближённая замена достаточно сложного объекта более простой моделью, которую удобнее изучать.

Геометрическая интерпретация пути.Путь, пройденный телом при любом движении, равен площади под графиком скорости на заданном промежутке времени.

Посмотрим, как работает эта геометрическая интерпретация в важном частном случае равноускоренного движения.

Задача. Тело, имеющее скорость в начальный момент , разгоняется с постоянным ускорением . Найти путь, пройденный телом к моменту времени .

Решение. Зависимость скорости от времени в данном случае имеет вид:

(2)

График скорости – прямая, изображённая на рис. 5. Искомый путь есть площадь трапеции, расположенной под графиком скорости.

Рис. 5. Путь при равноускоренном движении

Меньшее основание трапеции равно . Большее основание равно . Высота трапеции равна . Поскольку площадь трапеции есть произведение полусуммы оснований на высоту, имеем:

Эту формулу можно переписать в более привычном виде:

Она, разумеется, вам хорошо известна из темы “Равноускоренное движение”.

Задача. График скорости тела является полуокружностью диаметра (рис. 6). Максимальная скорость тела равна . Найти путь, пройденный телом за время .

Решение. Как вы знаете, площадь круга радиуса равна . Но в данной задаче необходимо учесть, что радиусы полуокружности имеют разные размерности: горизонтальный радиус есть время , а вертикальный радиус есть скорость .

Поэтому пройденный путь, вычисляемый как площадь полукруга, равен половине произведения на горизонтальный радиус и на вертикальный радиус:

Рис. 6. К задаче